ISO 12647-2:2013 : ∆E2000 versus ∆E76
- NormaPrint
- Temps de lecture : 8 minutes
L’ISO 12647-2 version 2013 fournit désormais les tolérances colorimétriques pour les aplats cyan, magenta, jaune et noir sous deux formes : en ∆Eab (Delta E 76) et en ∆E00 (Delta E 2000). Bien que les valeurs de tolérance exprimées en ∆E00 ne soient données qu’à titre informatif, ce mode de calcul des différences colorimétriques ne manque pas d’intérêt. Voyons pourquoi.
La notion de delta E en matière de colorimétrie est née en 1976 en même temps que l’espace CIE L*a*b*. Elle sert à quantifier, dans cet espace LAB, la différence perçue entre deux couleurs. Abréviation du grec delta, utilisé en mathématique pour décrire une différence, et du terme allemand “Empfindung”, qui peut être traduit en français par “sensation”, un ∆E (∆E = 1) est censé exprimer la plus petite différence perçue entre deux couleurs.
Le CIE L*a*b*, rappelons-le, est une modélisation mathématique de l’ensemble des couleurs perçues par l’être humain. Il partage ce statut avec d’autres espaces colorimétriques modélisés eux aussi par la Compagnie internationale de l’éclairage (CIE), tels que le CIE RGB 1931 ou le CIE XYZ 1931, tous issus des mêmes travaux expérimentaux de John Guild et William David Wright à la fin des années 20 du siècle dernier. À la différence du CIE RGB 1931 et du CIE XYZ 1931, le CIE LAB 1976, n’est pas un espace linéaire. Le CIE L*a*b* représente les couleurs, sous la forme d’une sphère, selon une température de blanc de référence. Il donne la part belle aux valeurs a* et b* (exprimées selon une échelle de 600 niveaux chaque), qui marquent la teinte et la saturation des couleurs, tandis que l’échelle du L* (la luminance) ne comporte que 100 valeurs de dégradé. Il exploite la représentation colorimétrique des axes du CIE XYZ 1931, mais selon des fonctions mathématiques non linéaires (la courbe de correspondance entre les informations en entrée et en sortie de chaque canal n’est pas une droite). Ainsi les ingénieurs de la CIE ont-ils souhaité créer une représentation plus perceptuellement uniforme des couleurs, c’est à dire où la distance entre les coordonnées mathématiques de deux couleurs dans l’espace en trois dimensions du LAB représente, du mieux possible, la différence de perception de ces couleurs par l’oeil humain. Du mieux possible ne veut cependant pas dire parfaitement.
Le LAB, un espace colorimétrique perceptuellement uniforme, ou presque !
Loin d’être elle-même linéaire, la perception humaine des couleurs est d’une telle complexité qu’aucun espace colorimétrique ne peut prétendre pour l’instant la modéliser parfaitement. Dans l’ordre décroissant, nos yeux sont plus sensibles à la teinte (la couleur de la couleur), puis à la saturation (la pureté de la couleur, dite aussi chromaticité ou chroma, c’est-à-dire sa teneur en blanc ou en gris), puis enfin à la luminance (l’intensité lumineuse rapportée à la surface éclairée). Mais par ailleurs parmi les teintes, l’oeil est plus sensible aux verts qu’aux bleus ou aux rouges. Cela est dû, semble-t-il, au passé arboricole de l’espèce humaine qui a fait que, des trois types de cônes dont nos yeux disposent, ceux spécialisés dans les verts sont plus performants. Cela signifie qu’à luminance et saturation égales, nous distinguons beaucoup plus de détails et de nuances dans les couleurs contenant du vert que dans les autres teintes. Ajoutons à cela que plus les couleurs sont saturées, moins les différences nous apparaissent. À l’inverse, une petite différence dans la dominante d’un gris nous saute aux yeux ! Enfin, côté luminance, non seulement nos yeux sont moins sensibles dans les hautes et basses lumières que dans les demi-tons, mais en plus le phénomène connu sous le nom anglais de “crispening effect” fait en sorte que deux couleurs nous apparaissent plus contrastées si on les compare sur un fond de luminance proche de celle de ces couleurs, alors que les mêmes nous semblent très semblables si on les observe sous un fond blanc ou un fond noir.
Delta E version 1976
Pour calculer la différence entre deux couleurs dans l’espace LAB, le ∆E76 dit aussi ∆Eab utilise la formule euclidienne suivante (source : http://zschuessler.github.io).
Il s’agit simplement d’utiliser le théorème de Pythagore (le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés) dans un espace en trois dimensions.
Utilisé de la sorte, les imperfections du CIE L*a*b* en termes d’uniformité mathématique de la perception, se retrouvent dans la valeur calculée du ∆E76. Si l’importance relative de la luminance vis-à-vis de la saturation et de la teinte est correctement minorée, les autres facteurs de la relativité perceptuelle de notre vision ne sont peu ou pas pris en considération.
C’est pourquoi d’autres formules plus précises, mais plus complexes de ∆E ont été élaborées par la CIE comme le ∆E94 et le ∆E00, dont les noms rappellent naturellement les années de leur publication.
Delta E 2000, plus précis, mais plus complexe
En 2013, la nouvelle norme ISO 12647-2:2013, consacre donc le Delta E 2000 en exprimant les tolérances de la norme à la fois en ∆E76 (se sont d’ailleurs toujours ces valeurs qui sont normatives comme c’était déjà le cas auparavant), mais aussi en ∆E00. L’ISO 12647-2:2013 ne fait donc pas de l’utilisation du second une exigence, mais se contente de publier les valeurs de tolérance en ∆E00 à titre “d’information”.
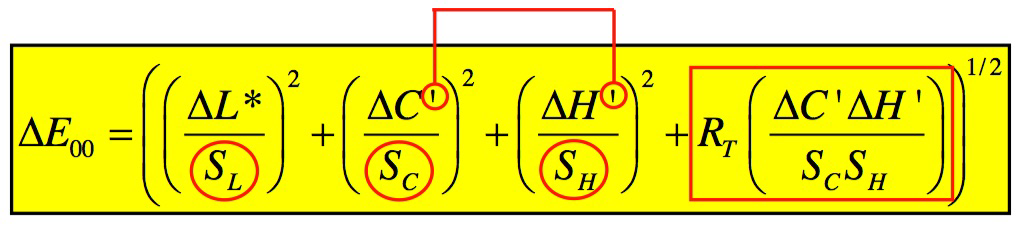
La formule du ∆E00 est la suivante (source : http://zschuessler.github.io) :
Le ∆E00 fait appel aux notions de ∆C et de ∆H qui expriment respectivement la différence de saturation (C pour chroma) et de teinte (H pour hue) entre les deux couleurs. La complexité de la formule exprime la volonté de pondérer (c’est-à-dire de compenser, de nuancer) les critères de teintes, de saturation et de luminance de façon à mieux prendre en compte les différences de perception de ces composantes par nos yeux. Alors qu’une tolérance exprimée en ∆E76 représente dans le LAB une sphère autour d’une couleur de référence, une tolérance exprimée en ∆E00 représente dans le LAB un volume elliptique en forme de ballon de rugby.
Les critères de pondération dans la formule du ∆E00 sont représentés par les termes SL, SC,SH et RT ainsi que par le signe prime (l’apostrophe) accolé aux ∆C et ∆H.
(source : ICC)
SL, SC et SH sont des valeurs calculées selon des fonctions matricielles pour compenser la non-linéarité de notre perception respectivement de la luminance, de la chromaticité et des teintes. Les différences de luminance, de chroma et de teinte entre deux couleurs sont donc ainsi pondérées selon ces fonctions avant d’être prises en compte dans le calcul du ∆E00. Les valeurs mêmes de chroma et de teinte sont elles aussi pondérées selon notamment qu’il s’agit d’une couleur peu ou très saturée (c’est ce qu’expriment les valeurs C’ et H’). Enfin le terme RT est un terme de rotation. Pour faire simple, il détermine quelle orientation prend l’axe de l’ellipse (le ballon de rugby) représentant le delta E dans l’espace en trois dimensions du LAB. Cette orientation est en effet différente selon que l’on s’approche ou que l’on s’éloigne de l’axe des gris.
Pour être complet, notons qu’un facteur “k” est également présent dans la formule du ∆E00. Celui-ci prend en compte les conditions d’observation.
kL=kc=kH=1 quand les conditions suivantes sont réunies (liste non exhaustive) :
- illuminant standard = D50
- flux lumineux = 1000 lx
- fond uniforme gris neutre avec L* = 50
- écart des couleurs mesurées < 5 ∆E*ab
- structure de l’échantillon homogène (pas de texture).
On le voit, le calcul d’un ∆E00 est autrement plus complexe que celui d’un ∆E76. Pour autant, en pratique, cette complexité n’est pas un obstacle, pour peu que l’on puisse faire confiance au logiciel qui le calcule. Certes, s’il est possible, à partir de deux valeurs LAB, de calculer leur ∆E76 à partir d’une simple feuille de calcul (voire avec une calculatrice), la même opération pour un ∆E00 nécessite de sérieuses connaissances mathématiques et une dextérité hors norme avec son tableur. Heureusement en salle de presse ou de prépresse, on utilise généralement un logiciel spécialisé. Pour peu que les développeurs de celui-ci n’aient pas fait d’erreur dans la programmation de la formule, utiliser un ∆E00 plutôt qu’un ∆E76 ne pose aucun problème notable et est autrement plus précis et fonctionnel.
En clair, grâce à ses fonctions de pondération intégrées, lorsque le ∆E00 concerne la comparaison entre deux couleurs dans des zones critiques du LAB (celles où notre vision est la plus aiguisée), la formule utilisée sera très exigeante (et le ballon de rugby représentant une unité de ∆E00 très petit), tandis que pour d’autres zones représentant des nuances pour lesquels nos yeux ne sont que peu sensibles, la formule utilisée sera plus lâche (et par conséquent le ballon de rugby d’un ∆E00 plus gros).
Né il y a bientôt 15 ans, le ∆E00 sort de sa période d’expérimentation pour rentrer en phase d’exploitation. Son efficience accrue vis-à-vis de son grand frère le ∆E76 devrait le voir s’imposer petit à petit en contrôle de production de l’imprimé.